En este análisis presentamos la quinta publicación de The Economist sobre las más importantes teorías económicas explicadas de una manera no ‘matematizada’ y con énfasis en cómo estas teorías se aplican en la actualidad.
Este artículo se refiere a la teoría de juegos, un estudio de las estrategias que se llevan a cabo en juegos complejos. Fue la mayor contribución del matemático John Forbes Nash (1928-2015), que murió el año pasado en un accidente de tráfico con su mujer, y cuya vida fue escenificada en el cine por Russel Crowe en una magnífica película: ‘Una mente brillante’. De hecho, el aporte de Nash a entender los comportamientos individuales y los resultados grupales, le sirvieron para ganar el Premio Nobel de Economía en 1994.

La teoría de juegos es hoy una rama de las matemáticas (muy usada por los economistas) que intenta formalizar situaciones donde existe una interacción estratégica entre distintos actores. Primero se define quiénes participan, luego se describe qué decisiones puede tomar cada protagonista y cómo las toma y, por último, se evalúan todos los resultados posibles de la interacción. El gran aporte de Nash fue brindarnos un concepto de la existencia de un equilibrio en todo tipo de situaciones: donde nadie se arrepiente de lo que hizo, dado que lo ‘hicieron’ los otros.
Un ejemplo de la no aplicación del equilibrio de Nash se daba en la industria de cerveza del Reino Unido. Este era un mercado con muchos jugadores, todos ellos trataban de crecer anticipándose a sus competidores y aumentaban su capacidad de producción. El problema es que todos hacían lo mismo y, por lo tanto, se producía una sobre oferta que diluía los márgenes y generaba quiebras masivas. A este resultado le seguía un mercado con poca oferta y altos márgenes, lo que volvía a ocasionar el incentivo para una nueva competencia autodestructiva en el camino a la sobre oferta. A este tipo de decisiones se les llama: “Macro silly decisions” (tontas decisiones macro). Después de muchos costos, la industria cervecera británica pudo alcanzar algunos equilibrios de Nash y evitar los ciclos destructivos.

Al demostrar matemáticamente que existen equilibrios en cualquier situación, Nash ayudó a economistas, políticos, burócratas y estrategas de negocios a entender el mundo que nos rodea de una mejor manera. Se formó la base de muchas de las estrategias vigentes que vemos por todo el mundo.
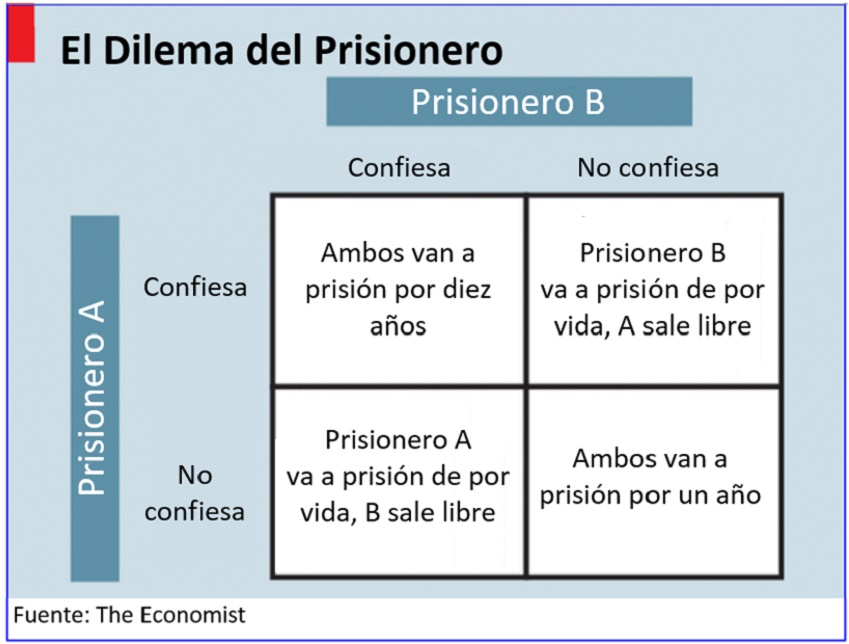
El ejemplo más conocido de la teoría de juegos es el del prisionero. En este caso, dos prisioneros cómplices que están aislados deben decidir simultáneamente si delatan a su compañero o no. Si ninguno delata, los dos van muy poco tiempo a prisión. Si uno delata a su compañero y el otro se queda callado, el delator queda en libertad y su compañero recibe una pena muy larga. Finalmente, si ambos se acusan mutuamente, los 2 van a prisión por un tiempo largo. Lo interesante aquí es que la situación en la que ambos se callan no es un equilibrio de Nash. Si mi compañero se quedó callado, yo querré delatarlo, y en ese caso a él no le habrá convenido quedarse callado. El equilibrio de Nash predice que ambos confesarán.
En el mundo real, tanto en las relaciones económicas como en las políticas y sociales, son muy frecuentes las situaciones en las que, al igual que en los juegos, su resultado depende de la conjunción de decisiones de diferentes agentes o jugadores. Tal vez un ejemplo mus sorprendente del equilibrio de Nash, es el del armamentismo nuclear durante la guerra fría que al basrse en el riesgo de destrucción mutua asegurada, generaba menores probabilidades de guerra.
¿Cómo se pueden cambiar los incentivos para que las personas, instituciones, empresas o grupos actúen de cierta forma, en que se obtengan mejores decisiones de grupo?
En el mundo real, los tomadores de decisiones individuales, no son necesariamente racionales. En los experimentos del dilema del prisionero, solo el 50% llega al equilibrio de Nash. Pero con mayor información y experiencia, se produce una convergencia positiva al equilibrio.
Lampadia
Teoría de juego
Escapando de prisión
La quinta publicación de la serie sobre las ideas económicas seminales ve el equilibrio de Nash
Por The Economist
20 de agosto 2016
Traducido y glosado por Lampadia

John Nash llegó a la Universidad de Princeton en 1948 para iniciar su (PHD) doctorado con una recomendación de una sola frase: «Es un genio de las matemáticas». No defraudó. Con 19 años y habiendo llevado tan sólo un curso de economía, durante sus primeros 14 meses como graduado produjo el trabajo que, en 1994, le ganaría un premio Nobel de Economía por su contribución a la teoría de juegos.

El 16 de noviembre de 1949, Nash envió una nota de una página de largo a las Actas de la Academia Nacional de Ciencias, en la que expuso un concepto que desde entonces se conoce como el «equilibrio de Nash». Este concepto describe un resultado estable que resulta de las personas o instituciones que toman decisiones racionales basadas en lo que piensan que harán los otros. En el equilibrio de Nash, nadie es capaz de mejorar su propia situación cambiando de estrategia: cada persona lo está haciendo lo mejor posible, aunque eso no sea el resultado óptimo para la sociedad. Con una gran habilidad matemática, Nash demostró que cada «juego» con un número finito de jugadores, cada uno con un número finito de opciones para elegir, tendría por lo menos un equilibrio.
Su perspicacia expandió el estudio de la economía. En mercados de competencia perfecta, donde no existen barreras de entrada y donde todos los productos son idénticos, ningún comprador o vendedor individual puede influir en el mercado: nadie necesita prestar atención a lo que los demás hacen. Pero la mayoría de los mercados no son así: las decisiones de los competidores y clientes importan. Desde la subastas hasta los mercados de trabajo, el equilibrio de Nash le dio a la ciencia una manera de hacer predicciones del mundo real sobre la base de los incentivos de cada persona.
Un ejemplo en particular se ha vuelto el símbolo del equilibrio: el dilema del prisionero. Nash usó álgebra y números para exponer esta situación en un amplio ensayo publicado en 1951, pero la versión más familiar para los estudiantes de economía es más apasionante. (El tutor de tesis de Nash, Albert Tucker, la presentó en una charla que dio a un grupo de psicólogos).
Se trata de dos cómplices en celdas separadas, cada una contemplando el mismo trato ofrecido por el fiscal. Si ambos confiesan un sangriento asesinato, cada uno de ellos se enfrenta a diez años de cárcel. Si uno se queda en silencio mientras que el otro lo acusa, entonces, el soplón obtendrá una recompensa, mientras que el otro se enfrentará a una vida en la cárcel. Y si ambos se mantienen callados, entonces, cada uno de ellos se enfrenta a un cargo menor, y sólo un año en la cárcel (ver diagrama).
Sólo hay una solución en el equilibrio de Nash para resolver el dilema del prisionero: que ambos confiesen. Cada una es una mejor respuesta a la estrategia del otro; ya que el otro podría haber soltado la verdad, ya que decir la verdad evita toda una vida en la cárcel. La tragedia es que si tan sólo pudieran trabajar juntos, ambos podrían lograr una mejor recompensa.
El ejemplo ilustra que las multitudes pueden ser tontas, así como sabias; lo que es mejor para el individuo puede ser desastroso para el grupo. Este trágico resultado es muy común en el mundo real. Si fueran libres para saquear el mar, los individuos pescarían más de lo que es mejor para el grupo, agotando el stock de pescados. Los empleados que compiten para impresionar a su jefe al permanecer más tiempo en la oficina alentarán el agotamiento de los trabajadores. Los bancos tienen un incentivo para prestar más cuando los precios de las casas se disparan, en lugar de reducir los préstamos.
Los problemas de las masas
El equilibrio de Nash ayudó a los economistas a entender cómo las mejoras para los individuos podrían dar lugar a consecuencias negativas para las multitudes. Mejor aún, les ayudó a resolver el problema: sólo tenían que asegurarse de que cada individuo se enfrentara a los mejores incentivos posibles. Si aún así las cosas siguen saliendo mal (como que los padres continúen sin vacunar a sus hijos contra el sarampión, por ejemplo), entonces debe ser porque las personas no estaban actuando en su propio interés. En tales casos, el desafío de las políticas públicas sería uno de mayor información.
La idea de Nash tenía antecedentes. En 1838, August Cournot, un economista francés, planteó la teoría de que en un mercado con sólo dos empresas, cada una de ellas sufriría las desventajas de buscar una mayor participación del mercado aumentando la producción, ya que esto causaría que los precios bajen y los márgenes de ganancias también sean menores.
Sin quererlo, Cournot había tropezado con un ejemplo del equilibrio de Nash. Tenía sentido que cada empresa establezca los niveles de producción basados en la estrategia de su competidor; los consumidores, sin embargo, terminarían con menos bienes y precios más altos si hubiera prevalecido una competencia despiadada.
Otro pionero fue John von Neumann, un matemático húngaro. En 1928, el año en que Nash nació, von Neumann esbozó una primera teoría formal de juegos, demostrando que en un juego de suma cero con dos personas, siempre habría un equilibrio. Cuando Nash compartió su hallazgo con von Neumann, para entonces un semidiós intelectual, este último desestimó el resultado como «trivial», viéndolo como poco más que una extensión de su propia prueba anterior.
De hecho, el enfoque de von Neumann en un juego de suma cero con solo dos personas dejaba un conjunto muy limitado de aplicaciones para su teoría. La mayoría de estos ajustes eran de naturaleza militar. Uno de ellos fue la idea de la destrucción mutua asegurada, en el que se alcanza el equilibrio al armar a los adversarios con armas nucleares (algunos han sugerido que el carácter de la película Dr. Strangelove se basó en von Neumann). Nada de esto fue particularmente útil para pensar en la mayoría de situaciones (incluyendo la mayoría de los tipos de mercados) en el que la victoria de una de las partes no implica automáticamente la derrota de la otra.
Aun así, inicialmente los economistas tuvieron el mismo pensamiento que von Neumann, y en gran medida pasaron por alto el descubrimiento de Nash. Éste se dedicó a otras actividades matemáticas, pero su gran promesa se vio debilitada cuando, en 1959, comenzó a sufrir de delirios y paranoia. Su esposa lo hospitalizó; y tras su alta, se convirtió en una figura conocida en el campus de Princeton, que hablaba consigo mismo y hacía garabatos en las pizarras. Mientras luchaba con su enfermedad, sin embargo, su equilibrio se hizo cada vez más central en la disciplina económica. La proporción de artículos de economía que citan el equilibrio de Nash se ha multiplicado por siete desde 1980, y el concepto se ha utilizado para resolver una serie de problemas de políticas del mundo real.
Un famoso ejemplo fue el sistema de hospitales de EEUU, que durante la década de 1940 estaba en un mal equilibrio de Nash. Cada hospital quería recibir a los más brillantes estudiantes de medicina. Dado que este tipo de estudiantes eran particularmente escasos debido a la guerra, los hospitales se veían forzados a enviar ofertas a candidatos prometedores cada vez más temprano. Lo que era mejor para el hospital individual, resultó ser terrible para el colectivo de hospitales: tenían que contratar a los estudiantes antes de que hayan pasado todos los exámenes. Los estudiantes también lo odiaban, ya que no tenían la oportunidad de considerar distintas ofertas.
A pesar de las cartas y resoluciones de toda clase de asociaciones médicas, así como de los propios estudiantes, el problema fue resuelto correctamente solamente después de décadas de ajustes y, en última instancia, gracias al diseño de Elliott Peranson y Alvin Roth en 1990 (que más tarde ganaron su propio Premio Nobel de Economía). Hoy en día, los estudiantes presentan sus preferencias y se les asignan a los hospitales en base a un algoritmo que garantiza que ningún estudiante pueda cambiar sus preferencias previamente declaradas y ser enviado a un hospital más prestigioso que también quiera recibirlo, y ningún hospital puede salirse del sistema y tomar a un mejor empleado. El sistema aprovecha al máximo el equilibrio de Nash: todo el mundo está haciendo lo mejor que puede en base a lo que hacen los demás.
Otras aplicaciones de políticas incluyen la subasta del gobierno británico de licencias de operaciones de telecomunicaciones móviles 3G en 2000. Llamó a los especialistas en teoría de juegos para ayudar a diseñar la subasta utilizando algunos de los puntos de vista del equilibrio de Nash, y terminaron recibiendo unos £ 22.5 mil millones (US$ 35.4 mil millones), aunque algunos de los accionistas de los oferentes no estuvieron satisfechos con el resultado. Las percepciones de Nash también ayudaron a explicar por qué la adición de un camino a una red de transporte puede hacer que el tiempo de viaje sea, en promedio, más largo. Los conductores autónomos interesados en optar por la vía más rápida pueden no tener en cuenta su efecto en la prolongación de los tiempos de viaje de los demás, por lo que pueden terminar atascando una ruta. Un estudio publicado en 2008 encontró siete salidas en las carreteras en Londres y 12 en Nueva York, donde cierres podrían aumentar el flujo de tráfico.
Que empiece el juego
El equilibrio de Nash no habría alcanzado su estado actual sin algunos refinamientos de la idea original. Primero, en muchas situaciones, hay más de un posible equilibrio de Nash. Los conductores eligen qué lado de la carretera deben usar para conducir en relación al comportamiento de los demás conductores, con resultados muy diferentes, dependiendo de dónde viven; se mantienen a la izquierda en Gran Bretaña, pero a la derecha en Estados Unidos. Para decepción de los economistas más matematizados, el entendimiento de estrategia requiere el conocimiento de las normas y hábitos sociales. El teorema de Nash por sí solo no era suficiente.

Un segundo refinamiento involucró la adecuada contabilización de las amenazas no creíbles. Si un adolescente amenaza con escaparse de casa si su madre le quita su teléfono móvil, entonces hay un equilibrio de Nash, donde ella le da el teléfono para mantener la paz. Pero Reinhard Selten, un economista alemán que compartió el premio Nobel con Nash y John Harsanyi en 1994, argumentó que esto no es un resultado plausible. La madre debe saber que la amenaza de su hijo es vacía, ya que una noche en las calles sería peor que perder un celular. Ella debe confiscar el teléfono, obligando a su hijo a concentrarse en su tarea.
El trabajo de Selten le permitió a los economistas a reducir gradualmente el número de posibles equilibrios de Nash. Harsanyi abordó el hecho de que en muchos juegos de la vida real, la gente no está segura de lo que su oponente va a hacer. A los economistas se les haría complicado analizar las mejores estrategias para dos tortolitos que deben escoger un lugar mutuamente aceptable para una fecha sin tener idea de lo que el otro prefiere. Mediante la integración de las creencias de cada persona en el juego (por ejemplo, que piensen correctamente que al otro le gusta la pizza tanto como el sushi), Harsanyi hizo que el problema pueda resolverse. Un problema diferente siguió acechando. La capacidad de predicción del equilibrio de Nash descansa en el comportamientos racionales. Sin embargo, los seres humanos a menudo no están a la altura de este ideal. En experimentos que replican el dilema del prisionero, sólo la mitad de las personas eligieron confesar. Para los economistas que habían incrustado la racionalidad (y Nash) en sus modelos, esto era problemático. ¿Cuál es el propósito de crear buenos incentivos, si la gente no busca sus propios mejores intereses?
No todo está perdido. Los experimentos también mostraron que la experiencia hizo más prudentes a los jugadores; en la décima ronda, sólo alrededor del 10% de los jugadores se negaba a confesar. Esto le enseñó a los economistas a ser más cautelosos con la aplicación del equilibrio de Nash. Con juegos complicados, o aquellos en los que no tienen la oportunidad de aprender de los errores, sus ideas pueden no funcionar tan bien.
El equilibrio de Nash, sin embargo, cuenta con un rol central en la microeconomía moderna. Nash murió en un accidente automovilístico en 2015; para entonces, su salud mental se había recuperado, había reanudado su enseñanza en Princeton y había recibido un Nobel en reconocimiento de que las interacciones del grupo contribuyen más que cualquier individuo.
Lampadia